D12: Decimal fractions on a number line

Here we show the position of a decimal number on a scale or number line, and ask pupils to locate or identify related numbers. We've met similar tasks involving common fractions in Theme D08, especially Task 08E.

TASK 12A: Do pupils recognise that 0.3 is twice 0.15 and that 0.05 is one third of 0.15?

For the first part of the task, some pupils might decide that 0.3 is less than 0.15, on the basis that 3 is less than 15. The second part doesn't involve that potential difficulty, though some pupils might decide that 0.05 is a lot smaller than it really is, on the basis that it involve hundredths, which are tiny!

TASK 12B: Here the red arrow has been placed halfway between 0 and 0.7 and the brown arrow has been placed halfway between 0.7 and 1. So the arrows point to 0.35 and 0.85.

For the first part, some pupils might be reluctant to accept 0.35 as the answer, as 35 is larger than 7. This issue is less prominent in the second part, as 85 is greater than 7, but of course it is also greater than the number at the end of the scale, 1. Some pupils might side-step this issue by choosing 0.3 or 0.4 for the first part, and 0.8 or 0.9 for the second part.

TASK 12C: The aim of this task is to get pupils to think about the relative values of the numbers represented by the digits in successive decimal places. Some pupils' initial reaction might be that they can't make sense of numbers with so many decimal places.

In the first part, the desired number is 0.1 more than the given number. This difference, 0.1, is about one third of the given number - in reality it is slightly less, but if we are locating the position by eye, this lesser amount is insignificant.

In the second part, the desired number, 0.3, will be located slightly to the left of the given number, as shown in the diagram below- though the task does not ask for such a precise answer. It is likely that many pupils will overemphasise the difference between the numbers and place 0.3 further to the left.

TASK 12D: The number 0.19 is less than 0.2 (even though 19 is not less than 2), so its position will be to the left of 0.2 - but not by much: its distance from zero will be 19/20 of the distance of 0.2 from zero.
The point exactly halfway between 0 and 0.2 on the number line represent the number 0.1. The desired number, 0.109, will be to the right of that - but by a similar small amount!

The task only asks for the rough locations of 0.19 and 0.109. Nonetheless, it is interesting to see the precise locations, which are shown below:

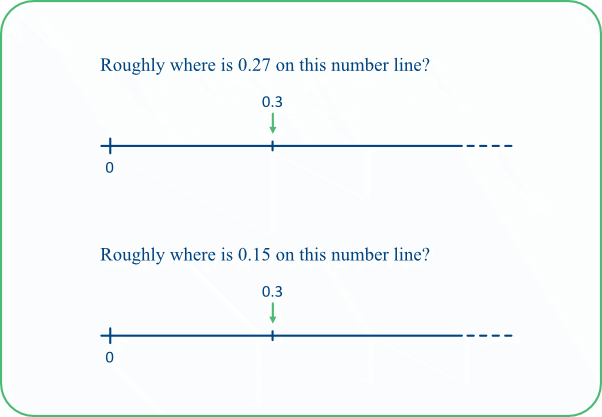
TASK 12E: In the first part, do pupils realise that 0.27 is less than 0.3? If so, do they locate the number's position intuitively or do they work in a more analytic way?  Some pupils might realise that 0.27 lies 9/10 of the way along the interval between 0 and 0.3.
In the second part, the number 0.15 lies halfway along the interval.

TASK 12F: The number 0.04 will be located 1/10 of the way along the interval between 0 and 0.4. For the second part, some pupils will know that 0.25 is the same as one quarter. However, this does not help much here, since we are not shown the whole interval from 0 to 1. One way to locate 0.25 is to locate 0.2 and 0.3 since it lies halfway between them.