D11: Fraction of a fraction as a decimal

Here we build on the previous Theme's ideas by considering how a diagram could be used to represent a fraction of a fraction as a decimal. There are practical limitations to this approach, as decimals involve 10ths, 100ths, 1000ths, etc, whose representation can be too small to draw clearly. Of course, that need not prevent pupils from imagining how an appropriate fractional part could be shown in a given diagram.

TASK 11A: The task asks pupils to explain how the diagram can be used to show that 3/4 of 3/5 can be represented by the decimal 0.45. Before addressing this fully, you might want to check that pupils have ways of evaluating 3/4 of 3/5 and that they can write the resulting fraction as a decimal.

Some pupils might calculate 3/4 × 3/5 = (3×3)/(4×5) = 9/20; they might then see that 9/20 = 45/100 and know that this can be written as 0.45.
Others might be able to discern that the small rectangles covering the dark yellow region are 20ths of the blue rectangle, and so the region represents 9/20; again, they might then see that 9/20 = 45/100 and know that this can be written as 0.45.

The dark yellow region covers 9 small rectangles, where each rectangle is one 20th of the blue square. We can combine pairs of the small rectangles to show tenths. (Why is that the case?). However, there will be one 20th left over. Can we partition this to show 100ths?

One solution is shown below left. Partitioning a rectangle representing one 20th into 5 equal parts, means each part represents one 100th. So we have four 10ths and five 100ths, which we can write as 0.45.
Another solution is shown below right: the dark yellow region is covered by 45 hundredths (perhaps seen as 10+10+10+10+5 hundredths). This can also be written as 0.45.

[With some classes it might be interesting to compare this geometric approach with a purely arithmetical one, by writing the original fractions as decimals. So 3/4 of 3/5 becomes 0.75 × 0.6. Does this give us 0.45?]

TASK 11B: Here the small rectangles covering the dark yellow region represent 40ths. So 1/4 of 7/10 is 7/40. Is that the same as 0.175?

We cannot readily combine the small rectangles to make tenths or split them to make 100ths, but we can split them to make 1000ths. One way to do that is shown below (it might be difficult for pupils to see the precise detail, and impractical for them to draw, but they might well be able to envisage what is going on). The small rectangles (40ths) have each been split into 25 equal smaller pieces, so that each small piece represents 1000ths. So the dark yellow region covers 7×27=175 thousandths; 175/1000 can be written as 0.175.

TASK 11C: Here the small square covering the dark yellow region is 1/16 of the blue square. Is that the same as 0.0625?

We cannot split the dark yellow square into 10ths of the large square, or 100ths or 1000ths, but we can split it into 10000ths, as shown below. How many 10000ths does it contain?

Note: 16 = 2⁴. Why does this tell us that 16 is a factor of 10000 but not of 10, 100, or 1000?

[You might want to relate the decimal for 1/16 to the decimals of more familiar fractions, for example 1/4 = 0.25 or 1/8 = 0.125. Do we get 0.0625 if we halve 0.125 or if we divide 0.25 by 4?]

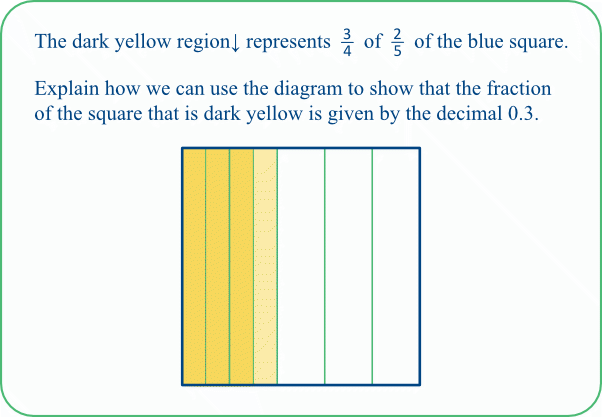
We end with a pair of much simpler tasks, both representing 3/4 of 2/5. Here we can read off the decimal from the diagram, without making further partitions. This is particularly straightforward for the second representation.

TASK 11D: Here the small rectangles represent 20ths. Pairs of these rectangles represent 10ths, three of which cover the dark yellow region, which therefore represents 3/10 of the large square. This can be written as 0.3.

TASK 11E: This again shows 3/4 of 2/5 but we have partitioned the 2/5 region into quarters in a different way. The dark yellow region is covered by three tall-thin rectangles, each half the width of the rectangles representing 5ths. So we again have 3/10 which is 0.3.