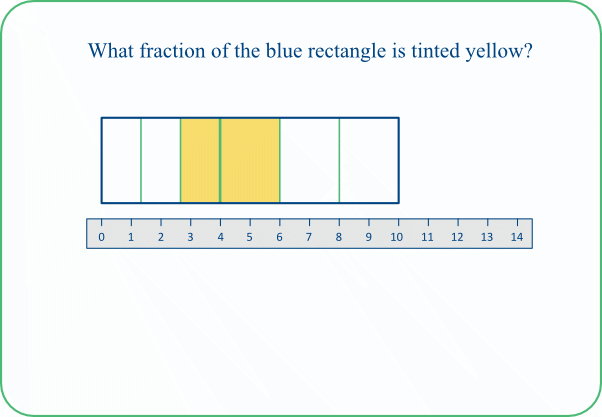
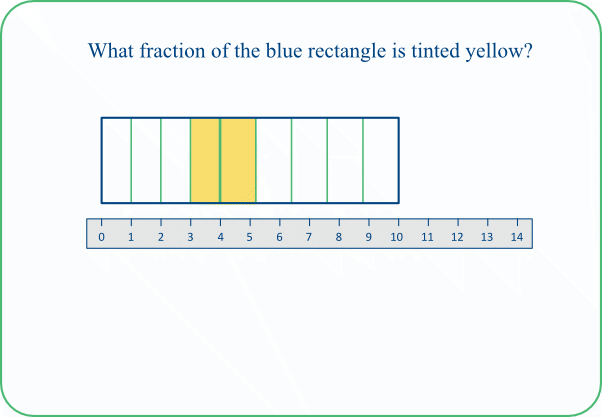
In these tasks we split a rectangle into two portions which are each partitioned into equal parts but where the parts for one portion are not the same as for the other. We include a ruler which can sometimes help us compare the parts. The tasks lend themselves to a variety of approaches which we can then compare and relate.
TASK 09A: The rectangle here has been split into a 2/5 portion and a 3/5 portion. In turn, these have been split into 2/15ths and 3/15ths respectively.
So the yellow tint covers 2/15 + 3/15 of the rectangle, which is 5/15 or ⅓.
Some pupils might notice that we can find the desired fraction ⅓ in a
much more direct way (using the distributive law, or 'French division'): ⅓ of the left hand portion is tinted yellow and one third of the
right hand portion is tinted yellow, so ⅓ of the two portions combined
is tinted yellow!
Formally: ⅓ of A + ⅓ of B = ⅓ of (A+B).
However, it is more likely that pupils will tackle the task by trying to find the fraction that each yellow part represents and then adding the fractions. This can be quite challenging as the whole rectangle is not partitioned uniformly. Consider the right hand portion; how readily do pupils see that this represents 6/10 or 3/5 of the whole rectangle? And do they see that one of its three parts will therefore be 6/30, 1/5 or 3/15 of the whole rectangle? Some pupils might notice that the right hand yellow part is 2 units wide, using the scale on the ruler, so it forms 2/10 or 1/5 of the whole rectangle. And some pupils might see that the yellow part as a whole is about 3⅓ units wide, which is about ⅓ of the total width. [The whole yellow part is, of course, exactly 3⅓ units wide - but how easy is it to show that?]
TASK 09B: This can be approached in similar ways to the previous tasks. Overall, ¼ of the blue rectangle is tinted yellow this time.
The rectangle has been divided on the left into tenths (2/5 ÷ 4) and on the right into 3/20ths (4/5 ÷ 5). These fractions might prompt pupils to work in decimals - or they could be asked to do so, in addition to using common fractions. Can pupils write 3/20 as a decimal? How might they attempt to add 0.1 and 0.15?
The ruler here is useful for 'measuring' the left hand yellow part, and perhaps for checking the answer, but it is more challenging to 'measure' the right hand yellow part.
TASK 09BC: One fifth of the rectangle is tinted yellow this time. We can again solve this directly (one fifth of the left portion plus one fifth of the rest is one fifth of the whole) or we can find the size of the separate parts and add.
The two yellow parts represent 2/25 and 3/25 of the rectangle which
again provides an opportunity to work in decimals alongside common
fractions. 2/25 is 8/100 which we can write as 0.08. But what about 3/25, which is 12/100? Do we write that as 0.12 or 0.012?
The ruler is useful here for checking the answer (2 units out of 10 units), but less so for 'measuring' the parts.
TASK 09BD: Here the two portions of the blue rectangle are split into different numbers of parts, so we can't use the 'direct' method based on the distributive law. We need to determine the fractions represented by the individual yellow parts.
The two yellow parts represent 1/10 and 3/25 of the rectangle, or 0.1 and 0.12. How can we add the common fractions? How can we add the decimals?
By thinking about the diagrams, we can see that the answer to this task must lie between the answers to the previous two tasks. Can we tell that by looking at the common fraction or decimal fraction answers?
[The answers for Tasks B, C and D are, respectively, ¼, ⅕ and ¹¹⁄₅₀ or 0.25, 0.2 and 0.22.]
In the current task, we have partitioned the left portion of the blue rectangle into 4 equal parts and the right portion into 5 equal parts. Say we did this the other way round. Instead of 4 and 5, say we did 5 and 4. Would this produce a smaller, the same, or larger yellow region?