This theme can be thought of as an interlude. Rather than looking at tasks, I discuss ways in which pupils might view fractions, especially early on.
Fractions can be interpreted in different ways (see, for example, Kieren, 1980): as a part-whole relationship, a ratio, division (or sharing), an operator, and a measure (or number). The focus early on tends to be on part-whole and/or sharing, and it is these that I want to discuss in more detail.
Nunes and Bryant (2009) suggest that "there are two types of situation in which fractions are used in primary school". The first involves measurement, the second involves sharing. One can see how both of these can arise, and develop, out of pupils'everyday experiences - for example, using a rod to measure one's height, and finding that the result is not an exact multiple of the rod; or sharing sticks of seaside rock and finding that one has to break some of the sticks if the shares are to be fair.
In practice, the focus with regard to measurement often reduces to finding quantities less than one, in other words considering parts of a single whole, such as one rod or one bar of chocolate. This narrowing can make the measurement activity seem less purposeful, but this part-whole view of fraction does have its affordances. The 'scheme of action' for representing a fraction in this way is fairly straightforward (in theory, if not in practice):
partition the whole into a desired number of equal parts, and select a certain number of the parts.
So, for example, 3/4 can be represented by partitioning a rod or bar or rectangle into 4 equal parts, each of which represents one quarter, and selecting (eg by shading) 3 of them. Of course, it is important here that pupils attend to the requirement that the parts are equal (even if not identical) and that this property is rendered with sufficient accuracy if, for example, they want to compare fractions using drawings. A Year 8 student who produced the drawing below, concluded, from the left hand portion of the drawing, that 1/3 was greater than 2/6. (If he had focussed on the right-hand portion, he might have concluded that 1/3 is less than2/6!)
[Note: I can't remember how it came about that the 6ths were labelled 2/6ths!]
The part-whole interpretation leads quite nicely to the notion of equivalent fractions. For example, having represented the fraction 3/4 by partitioning a 'whole' into 4 equal parts and shading 3 of them, it is not too difficult to see that if each part is now partitioned into, say, 7 equal parts, we end up with 7 times as many shaded parts than before and 7 times as many parts altogether. In other words, 3/4 is the same as 21/28.
The part-whole interpretation also lends itself quite well to the multiplication of fractions, as in the representations below for 2/5 of 3/4. In the first diagram, some work is still required to quantify the doubly-shaded region, namely that it represents 6/20. [I would argue that this offers a worthwhile challenge since the process of resolving it can be quite illuminating!] The actual quantity is more obvious in the second drawing, where we can see that each quarter is partitioned into 5 equal parts, which means 4×5 = 20 such parts would be needed to fully cover the whole.
One thing that the part-whole interpretation does not do very well is to show that the fraction 3/4, say, can be thought of as 3÷4 (or, at least, as the result of the operation 3÷4). This might seem rather odd! For people with a reasonable grasp of mathematics (but perhaps not of mathematics teaching) it might seem obvious that the two notions are inseparable, or indeed one and the same thing: 3/4 is 3÷4.
The part-whole interpretation can be seen as involving division, but in the case of 3/4, for example, we are at best dividing 1 by 4 rather than 3 by 4. We can express the scheme of action as 'divide 1 by 4, then multiply by 3' or 1÷4×3 (working from left to right). Of course, we can use our formal mathematical knowledge to show that this is equivalent to 1×3÷4, or simply 3÷4, but schematically they are not the same, as shown in these diagrams:
The sharing interpretation of fraction takes division as its starting point and leads to the fact that, for example, dividing 3 by 4 results in the quantity three quarters. Thus it takes us from 3÷4 to 3/4 and we might therefore want to say they are the same: 3÷4 = 3/4.
However, from the pupil's point of view, the relation might be far from obvious and the journey from the sharing situation represented by 3÷4 to the sharing outcome represented by 3/4 might be quite an adventure taking quite a lot of time.
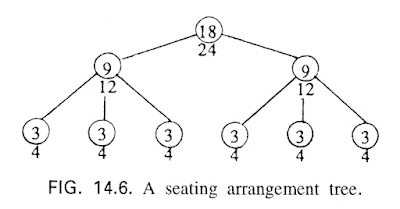
Streefland (1991, 1997), in a classic study, engaged students with the familiar idea (in Holland) of people sharing pancakes in a restaurant. He starts qualitatively, with questions about the fair share that each person would get if there were more pancakes than people or fewer pancakes than people. Then, when he starts to consider actual numbers of pancakes and people, for example 18 and 24, rather than going straight to the sharing outcome, he considers equivalent 'table arrangements' and how these can by symbolised. A key idea here is that if we put the pancakes and people into identical table arrangements then the resulting individual share will always be the same: one table of 18 pancakes and 24 people produces the same fair share as two tables of 9 pancakes and 12 people, or six tables of 3 pancakes and 4 people (and, ultimately, lots of tables of 3/4 pancakes and 1 person!). Note how the arrangements model equivalent fractions - though they might be better thought of as ratios (or rates).
In Streefland's study, the pupils, guided by the teacher, developed a symbol system for the table arrangements which foreshadowed our fraction notation but was distinct from it. An example is shown below, for a family of table arrangments (from Streefland, 1997, p354). Having similar notation gave pupils a 'natural' path to our abstract-seeming notation. Having distinct notation made it easier to distinguish between the sharing situation and the sharing outcome, though of course these two aspects are intimately connected.
The journey involved in finding the actual size of each share can be very rich. For example, with 3 pancakes shared fairly between 4 people, we can distribute the pancakes in ways such as these:
Method 1 illustrates a powerful basic approach: Try to give everybody one half of a pancake, then share out the rest.
Method 2 might emerge through trial and improvement, or through somehow knowing the size of the fair share in advance. The same goes for Method 3.
Method 4 is perhaps the simplest method - share the pancakes one at a time. It always works (though the pieces would be very small if there are lots of people!). It also shows very clearly what each total share comes to, in this case one quarter of a pancake times 3, the number of pancakes, making 3/4 of a pancake in all. So 3÷4 is equivalent to 1÷4×3, which gives us 3/4 and is similar to the way we arrive at 3/4 using a part-whole interpretation.
It might be thought we should simply focus on Method 4, as this shows very clearly and directly that 3 ÷ 4 produces a share of 3/4 or, in general, a ÷ b produces a share of a/b. However, the 'less direct' methods can be very enriching, by giving pupils experience of forming, comparing and combining fractions.
The task below (kindly posted on Twitter by Bernie Westacott) comes from a book published in Singapore: My Pals are Here 5 ( aimed at pupils equivalent in age to Year 6 in England, the last year of primary school). The diagram is ambiguous - it is not clear how the one-third pieces are distributed to the 3 pupils. This could lead to an interesting class discussion. On the other hand, the process could be conveyed in a cut-and-dried, non-exploratory way, and with the key statement '2 divided by 3 is the same as 2/3' being recited without much insight. It would be interesting to see what advice is offered in the Teacher's Guide about the experiences pupils might have had prior to this task.
Note: In a context like sharing pancakes, an argument can be made that the emerging families of ratios (that are formed, for example, when considering equivalent table arrangements) are more accessible than the resulting quantities when these quantities are fractions rather than whole numbers. So, when introducing fractions, perhaps we should devote more time than we usually do to the notion of fraction as ratio, as opposed to fraction as a measure or number!
Note2: Strictly speaking, we're talking of rates here (pancakes per persons) rather than pure ratios....
References
Kieren, T. E. (1980). The rational number construct - its intuitive and formal development. In Recent Research on Number Learning, edited by T. E. Kieren. Columbus, OH: ERIC/SMEAC.
Nunes, T. & Bryant, P. (2009). Key understandings in mathematics learning, Paper 3. London, Nuffield Foundation.
Streefland, L. (1991). Fractions in Realistic Mathematics Education. A Paradigm of Developmental Research. Dordrecht: Kluwer Academic Publishers.
Streefland, L. (1997). Charming fractions or fractions being charmed? In Nunes, T. & Bryant, P., Learning and Teaching Mathematics: an International Perspective. Hove: Psychology Press Ltd.
x