D24: Area and fractions

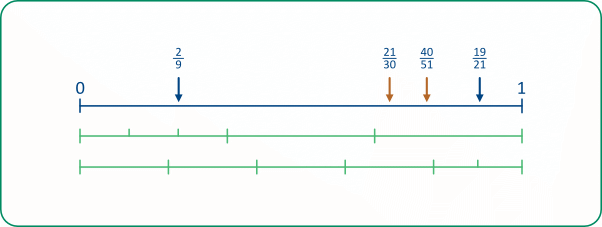
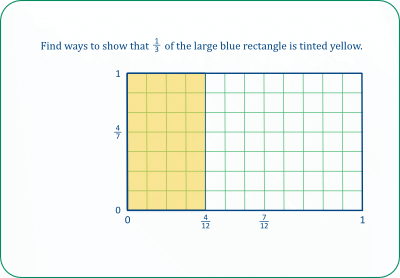
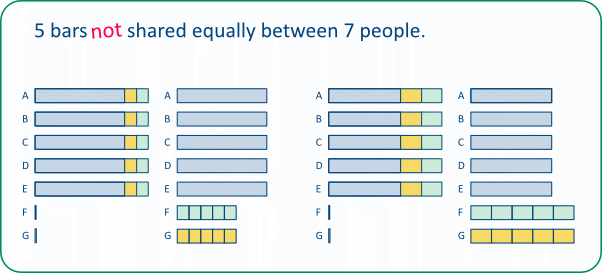
In this set of tasks we partition a square (or rectangle or parallelogram) systematically into smaller regions and express the areas of these regions as fractions of the area of the square. In a given task, the areas can be determined geometrically in a variety of ways; we can also use fractions to describe or determine areas, again in a variety of ways. So the tasks can provide pupils with plenty of experience of relating fractions to geometric shapes and of operating with fractions and comparing various fraction expressions and seeing their equivalence.

TASK 24A: There are many ways of solving this task. A simply approach would be to calculate the area of each region, using area formulae: The triangles can be thought of as having a base of 1 unit and a height of ⅔ unit, so they each have an area of ½×1×⅔ = ⅓ unit squares; similarly, we can think of the parallelogram as having a (vertical) base of ⅓ and a height of 1, so its area is 1×⅓ = ⅓. An interesting variant of this would be to find the area of the parallelogram and then deduce the areas of the triangles (if the parallelogram covers ⅓ of the square, then the two identical triangles must cover ⅔ of the square altogether, so ⅓ each). Or we could find the area of the triangles (each covers ⅓ of the square) and deduce that the remaining shape must therefore also cover 1 – ⅔ = ⅓.

The diagrams below show a variety of geometric approaches, whereby some of the regions of the square are transformed.

In (A), one of the triangles is transformed into a rectangle which clearly (!?) covers ⅓ of the square (so the other triangle also covers ⅓ and so the third region does too). We can also interpret the second diagram in (A) as showing how the parallelogram can be transformed into a rectangle using a shear.

In (B) the upper triangle is translated to join the other triangle, thereby forming a rectangle covering ⅔ of the square. So the remaining shape, which must have the same area as the original parallelogram, covers 1 – ⅔ = ⅓.

In (C-top) we have split each region into two triangles, with each triangle having the same area (½×⅓×1 = ⅙) OR (C-bottom) into 4 congruent triangles.

In (D) the given regions have been transformed into 3 identical parallelograms.

TASK 24B: This time the square is split into 7 regions, all with the same area. Notice that we again have 2 identical triangles, but this time there are 5 parallelograms, rather than 1. Can pupils see how this method of partitioning could be generalised to produce any number of regions with the same area?

TASK 24C: This is a fairly simple task, but which lends itself to a variety of approaches, both geometric and numerical.

The small, top-left triangle covers ⅛ of the square. We can visualise this by, for example, cutting the square into 4 congruent squares and halving one of them (see diagram below, left); or we could use the triangle area formula: ½×½×½ = ⅛. So the green region covers 1 – ½ – ⅛ = ⅜ of the square.

Or we could continue with a visual approach and argue that three such small triangles cover the green region, so it covers ⅛+⅛+⅛ = ⅜ of the square (see diagram below, middle).

We could also cut the green region into two triangles, each with a base of ½ and a height of 1 or of ½, so with a total area of ½×½×1 + ½×½×½ = ¼ + ⅛ = ⅜ (see diagram below, right).

TASK 24D: This again lends itself to a variety of approaches, both geometric and numerical.

A neat way to solve this is to partition the diagram into pairs of congruent white and green triangles, as below. This shows that the green region covers half the square.

Of course there are other, perhaps less neat, ways. For example, we could calculate the areas of the white triangular regions and subtract the total from 1:
area of white triangles = ½×1×⅓ + ½×1×⅔ = ⅙ + ⅓ = ½; so area of green region = 1 – ½ = ½.

Or we could partition the green region into a triangle and a parallelogram, giving a total area of
½×⅔×1 + ⅓ = ½.

TASK 24E: This is a variant on the previous task. We can again cut the green region horizontally to produce two triangles congruent to the white triangles. Or we could, for example, find the areas of the white triangles (giving us ⅟₇ + ⁵⁄₁₄ = ⁷⁄₁₄ = ½) and subtract this from 1.

TASK 24F: Another variant where the tinted region covers half the square.

Again, there are lots of ways of solving this. One approach is to make further cuts to produce matching white and green regions, as in the two examples below. We can, of course, also represent the various (green) sub-regions as fractions, giving us this set of expressions for the diagram below-right:
A + B + C = ⅕ + ⅕ + ⅟₁₀ = ⁵⁄₁₀ = ½.

A more direct approach would be to use the formula for the area of a trapezium: The green region is a trapezium with a (horizontal) height of 1 and with parallel sides of length ⅖ and ⅗, whose mean is ½, giving ½×1 = ½.

An interesting way to vary the task is to slide the vertical parallel sides along the edges of the square, as in the ways below. We know that the desired fraction is still ½, as we haven't changed the dimensions of the trapezium, but can we confirm this using geometric or fraction methods?

TASK 24G: This is very much more challenging, You might start by asking pupils to estimate what fraction of the square is tinted green. (How do they go about this? Do they mentally compare the green region to familiar fractional regions?)

The diagram below shows a geometric solution, where we think of the square as partitioned into parallelograms congruent to the green region. Altogether there are six, so the green region covers ⅙ of the square.

Here is a more analytic approach:
The equally spaced parallel red lines (below) cut the brown line into 3 equal parts.
So we can think of the green region as two triangles with a combined (horizontal) height of ⅔ and sharing a (vertical) base of ½. So their total area is ½×½×⅔ = ⅙.

TASK 24H: This is essentially the same as the previous task. We have changed the outer square into a parallelogram by means of a shear or stretch, or both. Parallel lines remain parallel, midpoints remain midpoints. We could have done the same to all the earlier tasks.

The tinted region is still ⅙ of the outer shape, and we can use the same methods as before to show this.
 

D23: The mediant of a pair of fractions

Here we look at the mediant of two fractions a/b and c/d. It is defined as (a+c)/(b+d). It turns out that mediant always lies between the two given fractions but is not necessarily equal to the mean.

When pupils attempt to add two fractions, they sometimes inadvertently find the mediant rather than the sum: the classic ½ + ⅓ = ⅖ misconception. You might feel that introducing pupils to the mediant could reinforce that misconception. On the other hand, the tasks in this theme encourage pupils to think carefully about the size of the fractions involved and thereby should help pupils develop their intuition about how the numerator and denominator affect the size of a fraction. In turn this should help pupils interrogate statements like ½ + ⅓ = ⅖: careful inspection reveals that ⅖ cannot be the sum of ½ + ⅓ since ⅖ is less than one of the addends. 

TASK 23A: Here we show the meaning of 'mediant' by means of an example. It should be said that an example alone does not define mediant unequivocally - we could invent other rules that lead to 5/9, given the fractions ⅖ and ¾.

Some pupils will find this task quite challenging. It might not be immediately obvious that the mediant ⁵⁄₉ lies between the given fractions ⅖ and ¾. One way to determine this, of course, is to transform the fractions into equivalent fractions with the same denominator. This can be a useful exercise for some pupils, but is fairly heavy going - the lowest common denominator is 180. Where the primary aim is to order the fractions, it can be illuminating to use 'benchmark' fractions like ⅓, ½, ⅔ and ¾. Pupils might discern that the fraction ⅖ is slightly less than ½ (for example on the basis that 2.5/5 is one half), while ⁵⁄₉ is slightly more than ½; at the same time, ⁵⁄₉ is less than ⁶⁄₉ or ⅔ and so is less than ¾.

TASK 23B: Here we change one of the fractions from Task 23A into an equivalent fraction where the numerator and denominator are much larger - what effect does this have on the mediant?

It will be interesting to see, in part a), whether any students have a sense that M₁ is less than M₂, because of the dominance of the numbers in the equivalent fraction B'.

It turns out that M₁ is the fraction 5/9, and M₂ is 14/21 or 2/3. The position of all four fractions is shown on the blue number line, below. It is not expected that pupils should be as precise- the primary aim is to put the fractions in the correct order. For example, 2/5 will be somewhere to the left of 1/2 (or 2.5/5) and to the right of 1/3 (or 2/6). The fraction 5/9 will be to the right of 2/5 - it is slightly larger than 1/2, but less than 2/3 (or 6/9).

TASK 23C: The fractions are slightly different from the previous task, but still small and fairly familiar, and we consider the mean as well as the mediant - they are usually not the same....

In part a), M₁ is again (slightly) less than M₂. The fraction M₁ is 5/11 (which is slightly less than 1/2) and M₂ is 8/15 (which is slightly more than 1/2).

The mean of fractions A and B is 29/56. How does that compare to 5/11 and 8/15? We could of course use common denominators here, or convert to decimals, but it is also nice to try to make use of benchmark fractions.

As mentioned above, 5/11 is slightly less than 1/2 and 8/15 is slightly more than 1/2 - but so is 29/56. More precisely, 8/15 is 0.5/15 or 1/30 more than 1/2, while 29/56 is only 1/56 more than 1/2. So the mediants and the mean, placed in order, are 5/11, 29/56, 8/15.

TASK 23D: This task emphasises the fact that the mediant and mean are not generally the same. However, they are in one special case - when the denominators are the same.

The lowest common denominator of the two given fractions is 28. If we write the fractions as 8/28 and 21/28, then it is easy to see that the mediant and mean are both 29/56.

TASK 23E: This task is a simple variant on Task 23B: the given fractions are less familiar and more 'extreme'. 

The numerator and denominator of 19/21 are much larger than those of 2/9, which has the effect of placing the mediant much closer to 19/21 than to 2/9. The numerator and denominator are larger still in 38/42, a fraction equivalent to 19/21, so the mediant moves even closer to 19/21.

The diagram below shows the position of the four fractions very precisely. However, one wouldn't expect such a precise response from pupils. 

One can again get a good estimate by using benchmark fractions. Indeed, this is a rich activity.
For example, one could estimate the position of 2/9 by estimating one third of the line, and then two thirds of that;
the fraction 21/30 is the same as 7/10; it is also slightly larger than 2/3 (21/30 = 2/3 + 1/30);
40/51 is slightly less than 40/50 or 4/5;
19/21 is just 2/21 less than 1, or nearly 1/10.

An alternative is to use decimals:
the four fractions are approximately equal to 0.222, 0.7, 0.784 and 0.905.
It is nice to relate these decimals back to the fractions. For example, one can think of 0.222... as one fifth, plus one fifth of one fifth, plus.... The decimal 0.784 is close to 0.8 which is 4/5. And 0.905 is close to 0.9 which is 1/10 less than 1.

TASK 23F: This task might seem obvious to some pupils, but it won't be to others. It turns out that the mediant is a fraction equivalent to 2/5:
42/105 = (42÷21)/(105÷21) = 2/5.

This is an intriguing result: we have created an equivalent fraction using addition (of a sort) rather than the usual method of multiplying the numerator and denominator of a fraction by the same number.

Formally, we can write this:
a/b and ka/kb are equivalent fractions;
(a+ka)/(b+kb) = a(1+k)/b(1+k) = a/b.

TASK 23G: This is a version of a classic task. It is essentially asking, "What happens to the size of a fraction if we add one to the numerator and the denominator?" At first glance, many pupils will say the size is unchanged.

Compared to 40/100, we can think of 41/101 as having an extra piece, but where the pieces are slightly smaller. What does this do to the size of the fraction? If we think multiplicatively, then changing 40 to 41 is more of a change than changing 100 to 101. So 41/101 is larger than 40/100. More precisely, the multiplier that maps 40 onto 41 is 41÷40 = 1.025, which is larger than 1.01, the multiplier that maps 100 onto 101.

Another way to approach the task is to think of what happens if we repeatedly add 1 to numerator and denominator. At some stage we would, for example, get the fraction 1040/1100, at another stage the fraction 100040/100100: the fraction gets closer and closer to 1/1. So if we start with a fraction less than 1, it gets larger.

TASK 23H: There is a lot going on here! The tasks refers to fractions as points on the graph. However, fractions are really represented by lines. For example, any point on the line through the origin and point A can be thought of as a fraction equivalent to 2/5, the fraction at A. Note also that the steeper the line, the larger the fraction.

Point M represents the fraction 5/9 which is of course the mediant of the fractions represented by points A and B. The slope of the line through the origin and M lies between the slopes of the lines through the origin and A and the origin and B, so the fraction represented by M lies (somewhere) between the fractions represented by A and B. This will always be the case, for any two given fractions - a nice 'proof' that the mediant of any two fractions always lies between them.
[I remember Ken Ruthven presenting this elegant idea at a conference, which is probably the first time I met it.]

TASK 23I: This is quite advanced! Perhaps more for us as teachers, than for many of our pupils.

Consider the line x = 2, say, and the points A' and B' where it cuts the lines OA and OB (as shown in the diagram below). A' and B' represent fractions with the same denominator and which are equivalent to those represented by A and B (if we are happy to accept fractional numerators). The midpoint of A'B' represents a fraction equivalent to the mean of the fractions represented by A and B. This point is (just) below the brown line OM and so the mediant is greater than the mean.

It turns out that the mediant of the two given fractions is 5/11 and the mean is 13/30. How can we tell that 5/11 is greater than 13/30? We could use common denominators (giving us 150/330 and 143/330, say). Or we could relate the fractions to one half:
5/11 = 1/2 –0.5/11 = 1/2 – 1/22;
13/30 = 1/2 – 2/30 = 1/2 – 1/15.
So both fractions are less than 1/2 but 5/11 is closer.

This nice task was posted on Twitter by Erick Lee. It inspired my next task, which involves a fraction between ⅛ and ⅟₇.

 TASK 23J: This might seem rather strange at first, since we have a part-whole representation of fractions where the whole changes but the part stays the same.

Rectangle A represents ⅛, rectangle C represents ⅟₇ and B represents a fraction in between: ⅟₇.₅ or ²⁄₁₅. The latter is of course the mediant of ⅛ and ⅟₇.

TASK 23K: It is tempting to think that the mediant of ⅛ and ⅟₇ lies exactly halfway between the two fractions, especially as 7.5 is exactly halfway between 8 and 7. We address this in the current task.

The second diagram in this task is interesting. It works well in conveying what was done to rectangles A and C, but because of its small scale it doesn't really allow us to read-off the answer - we have to think it through! The key here is to consider the factors by which A and C are shrunk or stretched. They both change by the same (additive) amount, so proportionally, the smaller rectangle (C), and its tinted region, changes more. So the fraction represented by B (⅟₇.₅) is closer to A's fraction (⅛) than C's fraction (⅟₇).

Numerically, rectangle A is 7.5/8 or about 93.75% of its original width, while C is 8/7.5 or about 106.67% of its original width. 100–93.75=6.25 < 106.67–100=6.67.

To finish things off, it is quite nice to consider our three fractions as decimals (to 4 dp): 0.125, 0.1333, 0.1429.

The difference (to 3 dp) between neighbouring fractions is 0.008 and 0.010, so about one hundredth in each case.

Comments welcome

mietmau@gmail.com
@ProfSmudge

 

D22: Fraction of a fraction - switching numerators

This theme was inspired by the photo below, which appears on page 108 of an excellent book by Catherine Fosnot and Maarten Dolk (2002): Young Mathematicians at Work: Constructing Fractions, Decimals and Percents. 

[My copy is an ex-library book from the University of Winchester. The book is in excellent condition, so did no one ever read it? Perhaps they replaced it with something on Mastery....]

TASK 22A: This is based on the fractions shown in the photo. The book contains several, similar tasks.

A basic way of finding the desired fraction is to count squares: the yellow rectangle covers 12 grid squares, while the blue rectangle covers 72 grid squares. So the fraction is 12/72 = ⅙. 

Or: each grid square represents ⅟₇₂ (Why?). So the yellow rectangle represents 12 × ⅟₇₂ = ¹²⁄₇₂ = ⅙.

In the Fosnot and Dolk book, the focus is on multiplying fractions. We can think of the yellow region as ⅜ of ⁴⁄₉ of the blue square (or ⁴⁄₉ of ⅜), so the fraction is ⅜ × ⁴⁄₉ = ¹²⁄₇₂ or ⅙. Fosnot and Dolk make the point that we can also find the fraction by rotating the yellow rectangle (shown here by the pink rectangle), which gives us a new pair of fractions and a new product ⁴⁄₈ × ³⁄₉. Notice that the numerators and denominators are the same as before, but we happen to get 'nicer' fractions leading to this simpler product: ½ × ⅓ = ⅙. Notice too, that the existence of these simpler fractions means it is also easier to see that the pink rectangle covers one 6th of the blue rectangle, as in the diagram below.

Rotating a rectangle as we have done here won't always lead to fractions that can be simplified. However, where it does, as in the current task, it helps to explain how we could get directly from our first product, ⅜ × ⁴⁄₉, to the simpler ½ × ⅓. In effect, this shows that we can extend our rule for simplifying a single fraction (divide the numerator and denominator by a common factor) to simplifying a product of fractions (divide a numerator and the denominator of the same or another fraction by a common factor). 

Of course, there are other ways of deriving this rule, for example by using the associative and commutative laws, as here:
⅜ × ⁴⁄₉ = 3×⅛×⅓×⁴⁄₃ = 3×⅓×⅛×⁴⁄₃ = ⅛×⁴⁄₃, and so on.

TASK 22B: Here is a similar task (though not directly from the book).

Again, we can count squares, or multiply the given fractions. Or we can rotate the yellow square, as below, where we can fairly easily see that it covers ⅓ of the blue rectangle, and where we get the very simple product 1×⁴⁄₁₂ = 1×⅓ = ⅓.

TASK 22C: Another variant.

This time the fraction is one quarter:
15/60 unit squares, or  ³⁄₁₀ × ⅚  or  ⁵⁄₁₀ × ³⁄₆.
By rotating the rectangle we can see the quarter easily.

TASK 22D: A chance to meet an improper fraction....

We get one quarter again, as can be seen below.

TASK 22E: From here on, we go on a bit of a tangent - there are no fractions as such but the maths (which one could think of as involving proportion and scaling) is intriguing. 

The previous tasks could be said to use different horizontal and vertical scales - the length of a horizontal unit is different from the length of a vertical unit. The same thing is happening here: while the grid appears to be composed of small squares, they are actually 5 units wide and 7 units high.

The tinted rectangles both cover 10 grid 'squares' so their areas are clearly the same. Each grid square has an area of 5×7 unit squares, so each rectangle has an area of 10×5×7 = 350 unit squares.

Because the axes have different scales, the rectangles are not congruent despite looking as though they are. Their dimensions are 10 by 35 units (yellow) and 25 by 14 units (pink). Of course, 10×35 does not just happen to be the same as 25×14. They are equal because 10×35 = 2×5 × 5×7 has the same factors as 25×14 = 5×5 × 2×7. This is similar to the property of the earlier tasks, where the different pairs of fractions had the same two numerators and the same two denominators.

TASK 22F: These are the same two rectangles as in the previous task, but this time the axes have the same scale. We can see that the rectangles are clearly different. However, as we noted before, their areas are the same because 10×35 and 25×14 are composed of the same factors.

TASK 22G: This combines the previous two tasks. It shows how the diagram where the axes are drawn to the same scale (Task 22F) has been 'compressed' to make the rectangles look the same (Task 22E).

TASK 22H: This explores in greater depth the effect that 'compressing' the plane has on the way a shape looks.

This task is challenging! It might help to draw the pink rectangle in different orientations on a 'normal' grid, where the horizontal and vertical scales are the same. It turns out the the angles of rotation b and c are 45 and 90 respectively.

The diagram below-left is the same as the diagram above. The diagram below-right is the 'decompressed' version.

 

Comments welcome

mietmau@gmail.com
@ProfSmudge

D21: Fractions as division (sharing)

 In Theme 13 I looked briefly at how a fraction, in this case ¾, can be thought of as (or as the result of) the division 3÷4. I used the scenario of 3 pancakes shared between 4 people, with this diagram showing some of the ways it could be done:

 

In each of these examples, the objects (pancakes), or parts thereof, are distributed until there is nothing left. In this theme, I consider a slightly different approach, whereby some individuals are given a whole object (be it a pancake, as above, or a bar, as below). Parts of each object are then taken away and given to the individuals who had nothing. Here is the first example:

TASK 21A: Here we have the scenario of 5 bars (of some sort!) being shared equally between 7 people. Initially, the 5 bars are given to 5 of the 7 people, with two people having nothing; small, equal parts are now removed from each bar and distributed among the two people with nothing. The critical challenge is to determine how large these pieces should be so that everyone ends up with the same amount.

In the diagram (above) the size of the green and the yellow pieces is such that everyone ends up with the same amount - as can be seen in the third column of the diagram. Everyone gets the equivalent of 5 of the small pieces, and we can see, from the second and third columns, that 7 small pieces make up one bar.
So each piece is ⅟₇ of a bar and everyone gets ⁵⁄₇ of a bar.

I would argue that the diagram can be used to demonstrate this outcome very nicely. Of course, this begs the question of how the certain size of the small pieces was determined in the first place. The diagram below shows what happens if the chosen size of the pieces is slightly too small (left) o slightly too large (right).

TASK 21B: Here we consider a slightly simpler case - only one person is without a bar initially. Again, the diagram should allow pupils to deconstruct what has happened very nicely - this time each small piece is ⅙ of a bar and everyone gets ⅚. We can write the statement below.

5 bars shared between 6 people   =   5 ÷ 6   =   ⅚.

[The statement might seem almost too obvious to bother writing down. However, for younger pupils each of the two steps represents a significant achievement.]

The strength of the task, in particular its diagram, could be said to lie in the ease with which it allows one to analyse the result of a successful sharing process. If you want to encourage students to predict what will happen, as well as analyse the result, you could present them with one of these incomplete or less detailed versions of the diagram:

 or

TASK 21C: Here most pupils will know from the start that each person gets one half of a bar. So the interest in the task is not in finding the answer but in seeing how it emerges as this particular method of sharing plays out. 

The three pieces make ½ because each is ⅙.

TASK 21D: Here we are almost back to the first task, which showed 5 ÷ 7. The current task is perhaps slightly more complex as there are more people who start with nothing.

TASK 21E: This involves the same situation as in the previous task but shows a simpler, more orthodox way of sharing the bars. This time, the bars are cut into pieces before any are distributed and the bars are shared equally one by one among the given number of people. The method involves the same principle as Method 4 at the top of the page. The outcome is not very 'interesting' but the method always works, and shows very clearly how we can get from B ÷ P to B/P:  

P people get 1/P of each bar, and so if there are B bars they get B × 1/P = B/P of a bar altogether.