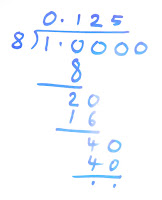Here we write the fraction ⅛ as a decimal fraction, using diagrams to help us. We also consider how we could write one tenth as an 'octal fraction', ie in terms of 8ths, 64ths, 512ths, etc.
TASK 01A: The scales here belong to two rather worn rulers. They show one inch divided into 10ths and 8ths.
Pupils can solve this at different levels. Many pupils will see that ½ is 5 tenths. Some who know that this can be written as 0.5 will also know that one half of that (¼) can be written as 0.25 and that one half of that (⅛) can be written as 0.125.
Other pupils might start on a similar path but get stuck at some stage and so have to look for ways of deriving the next step or steps. For example, some pupils might notice that ¼ is 2½ tenths. If so, their next step might be to think of ⅛ in a similar way (as 1¼ tenths). Or they might first look for a way to write ¼, or 2½ tenths, as a decimal. If so, do they approach this visually by imagining the tenths shown in the given diagram partitioned into a further 10 equal parts (ie into hundredths) or do they simply use the numerical fact that one tenth is 10 hundredths and so half a tenth is 5 hundredths? And do pupils work directly in hundredths (¼ = 25 hundredths = 0.25)? Or in tenths and hundredths (¼ = 2 tenths and 5 hundredths), and if so, do they see that this is the same as 25 hundredths?
Some pupils might know how to convert fractions into decimal fractions using a division algorithm, as here. If they adopt such an approach, it is worth relating it to the given diagram.
TASK 01B, TASK 01C: The diagram in the task above is not very detailed and it is worth asking pupils to think of a better diagram. Alternatively you might present them with one or other of these. How helpful are they?
TASK 01D: Or we could consider a diagram like this, where we revert to representing the fraction on a linear scale.
TASK 01E: The task below looks similar to our original task, but it is much more challenging. It is written for us rather than for use in the classroom, though it might work with some very much older, secondary school pupils. By 'octal fraction' we mean a fraction composed of 8ths, 64ths, 512ths, etc, in the same way that decimal fractions consist of 10ths, 100ths, 1000ths, etc.
One way to proceed would be by producing a more detailed diagram showing 8ths and 64ths, and perhaps even 512ths.
We can also approach the task in a more arithmetical way, starting like this:
One tenth is 6 64ths plus 0.4 64ths, which is 3.2 512ths;
this is 3 512ths plus 0.2 512ths, which is 1.6 4096ths;
and so on.
This gives us 1/10 = 0/8 + 6/64 + 3/512 + 1/4096 + ....
We can express this formally as here, where the divisor (10) is written in base 10 but the dividend and quotient are in base 8. Note that the octal fraction recurs, with the group of digits 6314 repeating for ever.
TASK 01F: Finally, something more straightforward: