D10: Fraction of a fraction

Here we use a (1 dimensional) bar, a (2 dimensional) rectangle and a (2 dimensional) Cartesian graph to model fraction of a fraction or the product of two fractions, in this case 2/3 of 5/7, or 5/7 of 2/3. 

Pupils are most likely to be familiar with the rectangle representation (or at least a version of it). They might find the other representations to be more challenging, though the representations should engage some pupils and might provide us, as teachers, with a fresh perspective!

Before embarking on some of the tasks below, you could start by simply asking pupils to 'Find 2/3 of 5/7': what methods do pupils spontaneously use? Or you could ask them to estimate the value - the answer is close to one half.

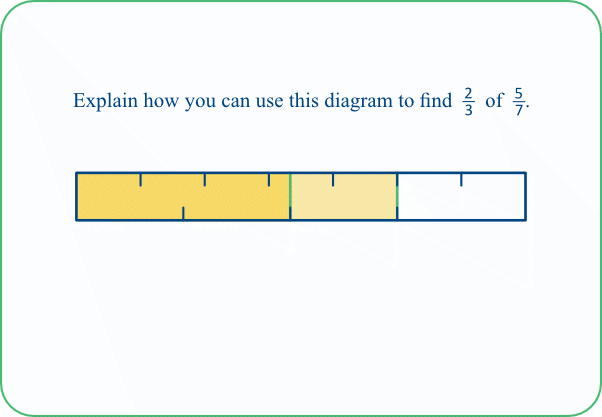
TASK 10A: Some pupils might need help with interpreting this at first! We can think of it like this:
5/7 of the bar is tinted yellow (as shown by the scale marked along the top of the bar),
and then 2/3 of that portion is tinted yellow again, producing a slightly darker yellow (as shown by the scale marked along the bottom of that part of the bar).
This latter portion represents the desired fraction.

We can see that the answer is very close to one half. We can get a precise answer by further partitioning the two scales into the same size parts on both scales. The result is shown below (Task 10B).
It can be seen that the dark yellow region covers 10 of the small parts, and we can determine (How?) that 21 such parts would be needed to cover the bar as a whole.
So the desired fraction is 10/21.

TASK 10B: This task is useful for discussiong the answer to Task 10A, and could be given to pupils who have found Task 10A too demanding. Pupils might still find the task challenging, since they need to determine how many of the small parts are needed to partition the bar as a whole.

We can see from the top scale that each 7th has been partitioned into 3 equal parts, so 7×3 = 21 such parts would be needed to partition the whole bar.

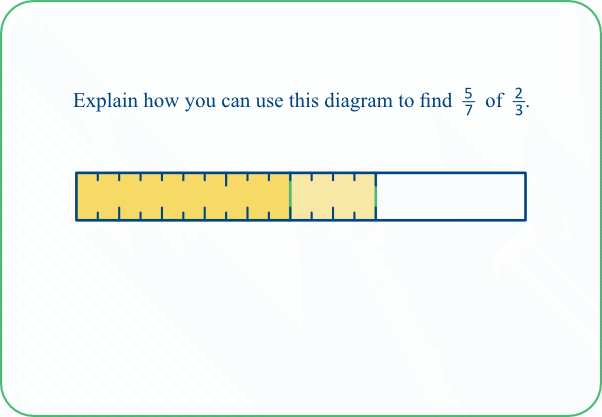
TASK 10C: Here we reverse the order of the fractions, so 2/3 of the bar is tinted first, and then 5/7 of the yellow portion is tinted again.

Again, we can find the precise value of the resulting fraction by partitioning the yellow part of the bar further, as shown in the version of the task below (Task 10D).

TASK 10D: Again, the challenge here is to find how many small parts would be needed to partition the whole bar. The top scale shows that each 3rd of the whole bar has been partitioned into 7 parts, so 3×7 = 21 parts would be needed in all.

TASK 10E: Here we use two dimensions, in the form of a rectangle, to show the combination of the two fractions. The rectangle is split in one direction to shown 5/7 and that portion is then split in a different direction of shown 2/3 of 5/7.

We can see quite easily that the resulting region (dark yellow) is split into 10 small equal parts, so it just remains for us to determine how many such parts would cover the original rectangle (21).

With a rectangle representation of this sort, it is more usual to split the whole rectangle in both directions, as in the diagram below. This makes it very easy to discern the number of small parts needed to cover the rectangle. However, we have deliberately not done this, for two reasons:
one, to emphasise that we are taking 2/3 of 5/7, not 2/3 of the whole rectangle;
two, to convey that our current focus is on sense making, including having to think about what is needed to express the result as a fraction, rather than perhaps just rushing to an answer that can be read off without too much thought.

TASK 10F: Here we reverse the order, by first taking 2/3 of a rectangle and then 5/7 of that. The result, of course, is the same.

 

TASK 10G: Here we take a far more abstract approach in that we represent our fractions (or at least the first one) by points on a straight line with a particular slope in the Cartesian plane. Older students might be intrigued by this and I hope it Fosters an interest in us too!

We represent 5/7 by a straight line through the origin and the point (7, 5). We can find equivalent fractions by choosing points on the line with whole number coordinates. One such point is (21, 15), whose y-coordinate, 15, can be nicely split into 3. Two-thirds of 15 is 10, giving us the point (21, 10) and the desired fraction 10/21.

TASK 10H: Here we represent 2/3 by points on another line in the Cartesian plane. This time the line goes through the origin and the point (3, 2).
We then choose a point on the line (representing a fraction equivalent to 2/3) where we can neatly find 5/7 of its y-coordinate, giving us 5/7 of the fraction's denominator. (21, 14) is such a point.
5/7 of 14 is 10, so, as before, we end up with the point (21, 10) representing the fraction 10/21.

Note: we have restricted ourselves to tasks where the desired fraction (10/21) can not be simplified. You might want to use tasks that do simplify (eg Find 5/6 of 2/3) to see what effect this property has on the various representations.