D12: Decimal fractions on a number line

Here we show the position of a decimal number on a scale or number line, and ask pupils to locate or identify related numbers. We've met similar tasks involving common fractions in Theme D08, especially Task 08E.

TASK 12A: Do pupils recognise that 0.3 is twice 0.15 and that 0.05 is one third of 0.15?

For the first part of the task, some pupils might decide that 0.3 is less than 0.15, on the basis that 3 is less than 15. The second part doesn't involve that potential difficulty, though some pupils might decide that 0.05 is a lot smaller than it really is, on the basis that it involve hundredths, which are tiny!

TASK 12B: Here the red arrow has been placed halfway between 0 and 0.7 and the brown arrow has been placed halfway between 0.7 and 1. So the arrows point to 0.35 and 0.85.

For the first part, some pupils might be reluctant to accept 0.35 as the answer, as 35 is larger than 7. This issue is less prominent in the second part, as 85 is greater than 7, but of course it is also greater than the number at the end of the scale, 1. Some pupils might side-step this issue by choosing 0.3 or 0.4 for the first part, and 0.8 or 0.9 for the second part.

TASK 12C: The aim of this task is to get pupils to think about the relative values of the numbers represented by the digits in successive decimal places. Some pupils' initial reaction might be that they can't make sense of numbers with so many decimal places.

In the first part, the desired number is 0.1 more than the given number. This difference, 0.1, is about one third of the given number - in reality it is slightly less, but if we are locating the position by eye, this lesser amount is insignificant.

In the second part, the desired number, 0.3, will be located slightly to the left of the given number, as shown in the diagram below- though the task does not ask for such a precise answer. It is likely that many pupils will overemphasise the difference between the numbers and place 0.3 further to the left.

TASK 12D: The number 0.19 is less than 0.2 (even though 19 is not less than 2), so its position will be to the left of 0.2 - but not by much: its distance from zero will be 19/20 of the distance of 0.2 from zero.
The point exactly halfway between 0 and 0.2 on the number line represent the number 0.1. The desired number, 0.109, will be to the right of that - but by a similar small amount!

The task only asks for the rough locations of 0.19 and 0.109. Nonetheless, it is interesting to see the precise locations, which are shown below:

TASK 12E: In the first part, do pupils realise that 0.27 is less than 0.3? If so, do they locate the number's position intuitively or do they work in a more analytic way?  Some pupils might realise that 0.27 lies 9/10 of the way along the interval between 0 and 0.3.
In the second part, the number 0.15 lies halfway along the interval.

TASK 12F: The number 0.04 will be located 1/10 of the way along the interval between 0 and 0.4. For the second part, some pupils will know that 0.25 is the same as one quarter. However, this does not help much here, since we are not shown the whole interval from 0 to 1. One way to locate 0.25 is to locate 0.2 and 0.3 since it lies halfway between them.

D11: Fraction of a fraction as a decimal

Here we build on the previous Theme's ideas by considering how a diagram could be used to represent a fraction of a fraction as a decimal. There are practical limitations to this approach, as decimals involve 10ths, 100ths, 1000ths, etc, whose representation can be too small to draw clearly. Of course, that need not prevent pupils from imagining how an appropriate fractional part could be shown in a given diagram.

TASK 11A: The task asks pupils to explain how the diagram can be used to show that 3/4 of 3/5 can be represented by the decimal 0.45. Before addressing this fully, you might want to check that pupils have ways of evaluating 3/4 of 3/5 and that they can write the resulting fraction as a decimal.

Some pupils might calculate 3/4 × 3/5 = (3×3)/(4×5) = 9/20; they might then see that 9/20 = 45/100 and know that this can be written as 0.45.
Others might be able to discern that the small rectangles covering the dark yellow region are 20ths of the blue rectangle, and so the region represents 9/20; again, they might then see that 9/20 = 45/100 and know that this can be written as 0.45.

The dark yellow region covers 9 small rectangles, where each rectangle is one 20th of the blue square. We can combine pairs of the small rectangles to show tenths. (Why is that the case?). However, there will be one 20th left over. Can we partition this to show 100ths?

One solution is shown below left. Partitioning a rectangle representing one 20th into 5 equal parts, means each part represents one 100th. So we have four 10ths and five 100ths, which we can write as 0.45.
Another solution is shown below right: the dark yellow region is covered by 45 hundredths (perhaps seen as 10+10+10+10+5 hundredths). This can also be written as 0.45.

[With some classes it might be interesting to compare this geometric approach with a purely arithmetical one, by writing the original fractions as decimals. So 3/4 of 3/5 becomes 0.75 × 0.6. Does this give us 0.45?]

TASK 11B: Here the small rectangles covering the dark yellow region represent 40ths. So 1/4 of 7/10 is 7/40. Is that the same as 0.175?

We cannot readily combine the small rectangles to make tenths or split them to make 100ths, but we can split them to make 1000ths. One way to do that is shown below (it might be difficult for pupils to see the precise detail, and impractical for them to draw, but they might well be able to envisage what is going on). The small rectangles (40ths) have each been split into 25 equal smaller pieces, so that each small piece represents 1000ths. So the dark yellow region covers 7×27=175 thousandths; 175/1000 can be written as 0.175.

TASK 11C: Here the small square covering the dark yellow region is 1/16 of the blue square. Is that the same as 0.0625?

We cannot split the dark yellow square into 10ths of the large square, or 100ths or 1000ths, but we can split it into 10000ths, as shown below. How many 10000ths does it contain?

Note: 16 = 2⁴. Why does this tell us that 16 is a factor of 10000 but not of 10, 100, or 1000?

[You might want to relate the decimal for 1/16 to the decimals of more familiar fractions, for example 1/4 = 0.25 or 1/8 = 0.125. Do we get 0.0625 if we halve 0.125 or if we divide 0.25 by 4?]

We end with a pair of much simpler tasks, both representing 3/4 of 2/5. Here we can read off the decimal from the diagram, without making further partitions. This is particularly straightforward for the second representation.

TASK 11D: Here the small rectangles represent 20ths. Pairs of these rectangles represent 10ths, three of which cover the dark yellow region, which therefore represents 3/10 of the large square. This can be written as 0.3.

TASK 11E: This again shows 3/4 of 2/5 but we have partitioned the 2/5 region into quarters in a different way. The dark yellow region is covered by three tall-thin rectangles, each half the width of the rectangles representing 5ths. So we again have 3/10 which is 0.3.

D10: Fraction of a fraction

Here we use a (1 dimensional) bar, a (2 dimensional) rectangle and a (2 dimensional) Cartesian graph to model fraction of a fraction or the product of two fractions, in this case 2/3 of 5/7, or 5/7 of 2/3. 

Pupils are most likely to be familiar with the rectangle representation (or at least a version of it). They might find the other representations to be more challenging, though the representations should engage some pupils and might provide us, as teachers, with a fresh perspective!

Before embarking on some of the tasks below, you could start by simply asking pupils to 'Find 2/3 of 5/7': what methods do pupils spontaneously use? Or you could ask them to estimate the value - the answer is close to one half.

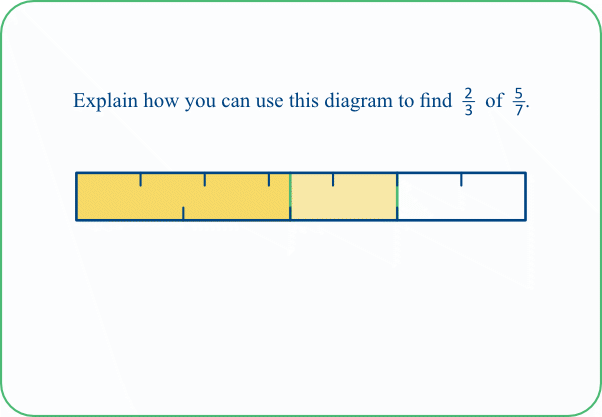
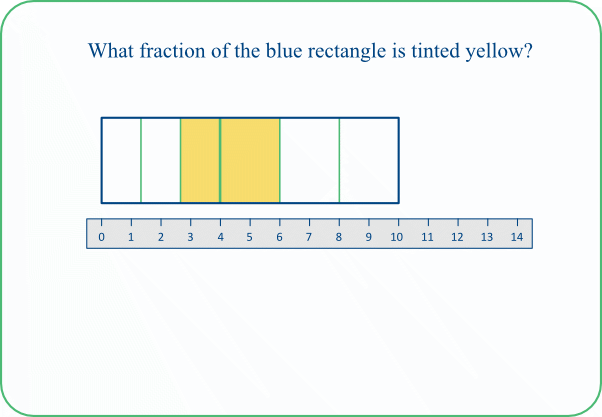
TASK 10A: Some pupils might need help with interpreting this at first! We can think of it like this:
5/7 of the bar is tinted yellow (as shown by the scale marked along the top of the bar),
and then 2/3 of that portion is tinted yellow again, producing a slightly darker yellow (as shown by the scale marked along the bottom of that part of the bar).
This latter portion represents the desired fraction.

We can see that the answer is very close to one half. We can get a precise answer by further partitioning the two scales into the same size parts on both scales. The result is shown below (Task 10B).
It can be seen that the dark yellow region covers 10 of the small parts, and we can determine (How?) that 21 such parts would be needed to cover the bar as a whole.
So the desired fraction is 10/21.

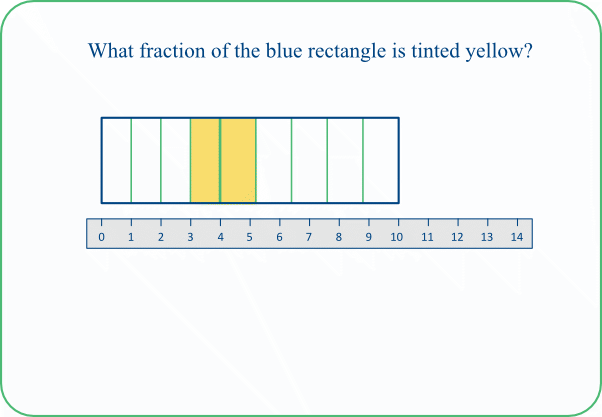
TASK 10B: This task is useful for discussiong the answer to Task 10A, and could be given to pupils who have found Task 10A too demanding. Pupils might still find the task challenging, since they need to determine how many of the small parts are needed to partition the bar as a whole.

We can see from the top scale that each 7th has been partitioned into 3 equal parts, so 7×3 = 21 such parts would be needed to partition the whole bar.

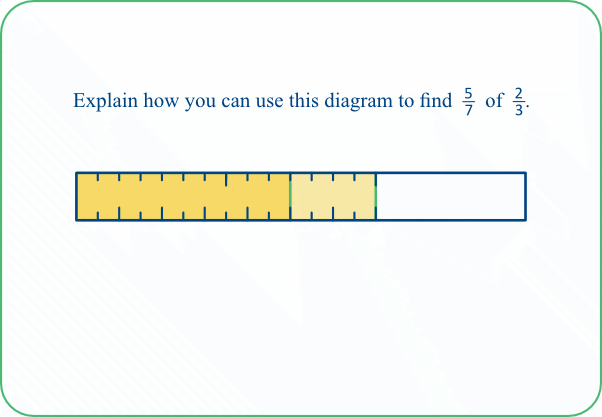
TASK 10C: Here we reverse the order of the fractions, so 2/3 of the bar is tinted first, and then 5/7 of the yellow portion is tinted again.

Again, we can find the precise value of the resulting fraction by partitioning the yellow part of the bar further, as shown in the version of the task below (Task 10D).

TASK 10D: Again, the challenge here is to find how many small parts would be needed to partition the whole bar. The top scale shows that each 3rd of the whole bar has been partitioned into 7 parts, so 3×7 = 21 parts would be needed in all.

TASK 10E: Here we use two dimensions, in the form of a rectangle, to show the combination of the two fractions. The rectangle is split in one direction to shown 5/7 and that portion is then split in a different direction of shown 2/3 of 5/7.

We can see quite easily that the resulting region (dark yellow) is split into 10 small equal parts, so it just remains for us to determine how many such parts would cover the original rectangle (21).

With a rectangle representation of this sort, it is more usual to split the whole rectangle in both directions, as in the diagram below. This makes it very easy to discern the number of small parts needed to cover the rectangle. However, we have deliberately not done this, for two reasons:
one, to emphasise that we are taking 2/3 of 5/7, not 2/3 of the whole rectangle;
two, to convey that our current focus is on sense making, including having to think about what is needed to express the result as a fraction, rather than perhaps just rushing to an answer that can be read off without too much thought.

TASK 10F: Here we reverse the order, by first taking 2/3 of a rectangle and then 5/7 of that. The result, of course, is the same.

 

TASK 10G: Here we take a far more abstract approach in that we represent our fractions (or at least the first one) by points on a straight line with a particular slope in the Cartesian plane. Older students might be intrigued by this and I hope it Fosters an interest in us too!

We represent 5/7 by a straight line through the origin and the point (7, 5). We can find equivalent fractions by choosing points on the line with whole number coordinates. One such point is (21, 15), whose y-coordinate, 15, can be nicely split into 3. Two-thirds of 15 is 10, giving us the point (21, 10) and the desired fraction 10/21.

TASK 10H: Here we represent 2/3 by points on another line in the Cartesian plane. This time the line goes through the origin and the point (3, 2).
We then choose a point on the line (representing a fraction equivalent to 2/3) where we can neatly find 5/7 of its y-coordinate, giving us 5/7 of the fraction's denominator. (21, 14) is such a point.
5/7 of 14 is 10, so, as before, we end up with the point (21, 10) representing the fraction 10/21.

Note: we have restricted ourselves to tasks where the desired fraction (10/21) can not be simplified. You might want to use tasks that do simplify (eg Find 5/6 of 2/3) to see what effect this property has on the various representations.

 

D09: Rectangles and rulers

In these tasks we split a rectangle into two portions which are each partitioned into equal parts but where the parts for one portion are not the same as for the other. We include a ruler which can sometimes help us compare the parts. The tasks lend themselves to a variety of approaches which we can then compare and relate.

TASK 09A: The rectangle here has been split into a 2/5 portion and a 3/5 portion. In turn, these have been split into 2/15ths and 3/15ths respectively.

So the yellow tint covers 2/15 + 3/15 of the rectangle, which is 5/15 or ⅓.

Some pupils might notice that we can find the desired fraction ⅓ in a much more direct way (using the distributive law, or 'French division'): ⅓ of the left hand portion is tinted yellow and one third of the right hand portion is tinted yellow, so ⅓ of the two portions combined is tinted yellow!
Formally: ⅓ of A + ⅓ of B = ⅓ of (A+B).

However, it is more likely that pupils will tackle the task by trying to find the fraction that each yellow part represents and then adding the fractions. This can be quite challenging as the whole rectangle is not partitioned uniformly. Consider the right hand portion; how readily do pupils see that this represents 6/10 or 3/5 of the whole rectangle? And do they see that one of its three parts will therefore be 6/30, 1/5 or 3/15 of the whole rectangle? Some pupils might notice that the right hand yellow part is 2 units wide, using the scale on the ruler, so it forms 2/10 or 1/5 of the whole rectangle. And some pupils might see that the yellow part as a whole is about 3⅓ units wide, which is about ⅓ of the total width. [The whole yellow part is, of course, exactly 3⅓ units wide - but how easy is it to show that?]

TASK 09B: This can be approached in similar ways to the previous tasks. Overall, ¼ of the blue rectangle is tinted yellow this time.

The rectangle has been divided on the left into tenths (2/5 ÷ 4) and on the right into 3/20ths (4/5 ÷ 5). These fractions might prompt pupils to work in decimals - or they could be asked to do so, in addition to using common fractions. Can pupils write 3/20 as a decimal? How might they attempt to add 0.1 and 0.15?

The ruler here is useful for 'measuring' the left hand yellow part, and perhaps for checking the answer, but it is more challenging to 'measure' the right hand yellow part.

TASK 09BC: One fifth of the rectangle is tinted yellow this time. We can again solve this directly (one fifth of the left portion plus one fifth of the rest is one fifth of the whole) or we can find the size of the separate parts and add.

The two yellow parts represent 2/25 and 3/25 of the rectangle which again provides an opportunity to work in decimals alongside common fractions. 2/25 is 8/100 which we can write as 0.08. But what about 3/25, which is 12/100? Do we write that as 0.12 or 0.012?
The ruler is useful here for checking the answer (2 units out of 10 units), but less so for 'measuring' the parts.

TASK 09BD: Here the two portions of the blue rectangle are split into different numbers of parts, so we can't use the 'direct' method based on the distributive law. We need to determine the fractions represented by the individual yellow parts.

The two yellow parts represent 1/10 and 3/25 of the rectangle, or 0.1 and 0.12. How can we add the common fractions? How can we add the decimals?

By thinking about the diagrams, we can see that the answer to this task must lie between the answers to the previous two tasks. Can we tell that by looking at the common fraction or decimal fraction answers?
[The answers for Tasks B, C and D are, respectively, ¼, ⅕ and ¹¹⁄₅₀ or 0.25, 0.2 and 0.22.]

In the current task, we have partitioned the left portion of the blue rectangle into 4 equal parts and the right portion into 5 equal parts. Say we did this the other way round. Instead of 4 and 5, say we did 5 and 4. Would this produce a smaller, the same, or larger yellow region?

D08: Dividing and multiplying fractions by a whole number

Here we look at some relatively simple division (and multiplication) tasks - in that the divisor (or multiplier) is a (small) whole number. One point of interest is whether pupils recognise that they can divide a fraction by operating on its denominator.

TASK 08A: In the first part of this task, the division can readily be performed by dividing the numerator by two or by doubling the denominator. Which will be more common? I imagine more pupils will opt for the former. The second part is likely to be more demanding as the numerator is odd - do the pupils who halved the numerator in the first part, switch to doubling the denominator in the second part? Some pupils might give the answer 8½/25, which could lead to an interesting discussion. Should we allow it?! Can we find an orthodox equivalent?

TASK 08B: This might be thought to be a bit of a trick question.... Careful scrutiny will show that the yellow strip in B is a quarter the size of the strip in A. But some pupils might opt for one third, as this leads to the nice, simple answer, ⅕.

TASK 08C: This is a more explicit version of Task 08B, but does that mean it is easier? It might still be demanding for some pupils to find a way to divide 3/5 by 4. And it looks as though it might be possible to partition the bar into a total 7 of the smaller pieces, leading to the answer ⅟₇ (which would in fact be a very good estimate, as it is very close to the correct answer, 3/20).

TASK 08D: Here each of the three given fifths has been divided by 4. Does that lead to the same result as in the previous two tasks? [This is an example of what Streefland calls French division. If 4 people decide to share 3 pizzas equally, do they get the same amount if the waiter brings the pizzas one at a time or all three at once?]

TASK 08E: Here we are just doubling and halving so it is fairly easy to locate the position of the fractions on the scale, but of course only if pupils realise that we are doubling and halving, and display the resulting fractions the right way round!

TASK 08F: This task is not adhering to the division theme, but it provides a nice challenge.

The first part can be solved by visualising one third of the given interval and moving the arrow on by that amount. Do pupils solve it that way or do they first try to divide the whole strip into 11 equal parts?

In the second part, do pupils realise that the desired fraction is to the right of the given fraction, and that the difference is 'small'!? 

Do any pupils attempt to solve this precisely? We can think of the strip as being divided into 110 equal parts, with 3/11 covering 30 of them and 3/10 covering just 3 more!
Put another way: 3/11 + 1/10 of 3/11 = 3/10.

TASK 08G: Here we are dividing and multiply the given fraction by 3. How readily do pupils realise that? The ruler allows us to locate the desired fractions precisely, although pupils might be thrown by the observation that the green rod is not an exact number of units long. As with earlier tasks, we can find the desired fractions without explicitly dividing the whole rod into equal parts.
 

TASK 08H: Here we sidestep the theme again, but make use of the ruler from the previous task. A relaxing task to round things off, with a moderate challenge offered by rod C.

There are some more tasks involving the ruler in the next section.
 

 

D07: Three quarters divided by two ninths

 Here we look at a range of ways we can model and solve ¾ ÷ ²⁄₉. Some of these tasks should work with some pupils, but the section is primarily aimed at us as teachers. How accessible do the approaches seem to be? Might we use them in class?

If you do decide to use some of the tasks in class, you might start by simply asking pupils how they might solve this and roughly what size of answer they expect. What range of ideas do the pupils come up with?

TASK 07A: We can estimate the value of the division by thinking of division as quotition or measurement. How many times does the brown segment fit into the yellow segment? We can fit in 3 of the brown segments with perhaps another 3/8 or so of the brown segment.

[We know, using formal methods that the actual answer is 3/4 × 9/2 = 27/8 which is indeed 3⅜!]

TASK 07B: Here we have added a line to the diagram in Task 07A to produce a double number line (DNL). We can see (and know from the previous task) that the number represented by '?' on the top scale is (about) 3⅜.

We can calculate the value by finding the number that scales ²⁄₉ to 1 and applying this scale factor to ¾. The scale factor is, of course (?!), ⁹⁄₂, the reciprocal of ²⁄₉, since ²⁄₉ × ⁹⁄₂ = 1.
And ¾ × ⁹⁄₂ = 27/8 = 3⅜.

TASK 07C: Here is an alternative DNL interpretation of the division. It can be thought of as partitive division or sharing: if ²⁄₉ of a share is ¾, what is 1 share?

Analytically, we can find the number that scales ²⁄₉ onto ¾ and apply this to 1. In practice, this takes us round in circles, unfortunately, since it is this very factor that the given division represents. However, we can solve the division by 'skipping along the number lines' using 'rated addition':
2/9 corresponds to 3/4, so 4/9 corresponds to 6/4, so 6/9 corresponds to 8/4, so 8/9 corresponds 12/4, and so 8/9 + 1/9 = 1 corresponds to 12/4 + 3/8 = 3⅜.

TASK 07D: A ratio table can be a useful way of organising multiplicative information, though it has lost the (geo)metric information carried by a double number line. Also, putting information into such a table is not always a trivial task. For example, in the given table, how do we know to put the '1' under 2/9 and not under 3/4?

We can solve the task by finding the 'horizontal' multiplier that maps 2/9 onto onto 3/4 and applying it to 1; or by finding the 'vertical' multiplier that maps 2/9 onto 1 and applying it to 3/4. Here, the vertical multiplier is perhaps easier to find as it is simply the reciprocal of 2/9. [Note that the latter provides us with a formal derivation of the turn it upside down and multiply rule: multiplying both terms in our given expression by 9/2 transforms it into (¾ × ⁹⁄₂) ÷ 1, or simply ¾ × ⁹⁄₂.]

TASK 07E: This task is asking pupils (or us) to work in quite an abstract way. However, it might be more accessible to some people than the pictorial models in the tasks above. [Though we could of course use the models to help us solve some of the steps.]

The result of the first line is 9. (Why?) In the second step we halve that (4½). We then divide by 4 (1⅛). Finally we multiply by 3 (3⅜).

TASK 07F: Here we work our way to the desired expression by leaving ¾ unchanged, in contrast to the previous task where 2/9 was left unchanged. Which progression is easier?

The result of step 1 leaves ¾ unchanged. In step 2 we divide by something 9 times as small so the result will be 9 times as large (27/4 or 6¾). In step 3 we halve the current result (3⅜).

TASK 07G: Here we start with the expression we want to evaluate and transform it into simpler but equivalent expressions. What is going on in each case?

TASK 07H: This is the first of three tasks where we use two dimensions to model our given expression, rather like a Cartesian graph with its orthogonal axes. This task's diagram bears a close resemblance to the DNL in Task 02B, where we can think of the lines as parallel axes.

There are lots of (closely related) ways of looking at this task, based on the fact that we have two similar triangles. If we use a 'measurement' interpretation like the one in Task 07B, we can say that the question "How many times does the brown segment fit into the yellow segment?" is equivalent to "How many times does the shorter green segment (of length 1) fit into the longer green segment (of length 3⅜)?"

TASK 07I: This relates quite closely to the DNL in Task 07C, which we interpreted in terms of 'sharing'. Here we could ask something like this: "If a triangle whose base is 2/9 of the base of a similar 'whole' triangle, has a height of 3/4, what is the height of the whole triangle?"

TASK 07J: Finally, we model the situation using a proper Cartesian graph, though whether it Fosters greater insight is perhaps a moot point!

We could, if we so wished, interpret the graph algebraically. For example, we could think of the slanting line as having the equation y = ²⁄₉x, or x = ⁹⁄₂y.
So when y = ¾, the value of our expression is given by the value of x at that point.
 

D06: Pairs of fractions on a bar or line

Here we look at fractions on a number line (or 'scale'), where the value of a fraction is give by how far it is to the right of 0. We restrict ourselves to the interval 0–1, ie to fractions less than 1, and we use a thin bar, rather than just a line, to make the representation more accessible to pupils.

TASK 06A: In this task, most pupils will probably realise that ⅟₇ is to the left of ¼, but at first they might feel that they don't have enough information to mark its exact position.

If pupils are stuck on the task, there is a good chance that they will hit upon the necessary insight if given time. The solution (below) is really quite simple - once one sees it! The quarter interval has been divided into 7 equal parts, so we can divide the whole 0–1 interval into 7×4 = 28 such parts, and so ⅟₇ will consist of 28÷7 = 4 such parts.

The task can, of course, also be solved in a more formal manner, by finding common denominators in a rule-based way. A strength of the task is that it can take pupils back to first principles and therefore throw light on a rule where pupils who have lost touch with the relationships on which the rule is based.

TASK 06B: This task can be used if you want to make the above explanation more explicit (by showing all 28 parts) - or if pupils are genuinely stuck on the first task.

TASK 06C: This is a more extreme version of the first task, and can be used to reinforce the ideas that emerged there.

TASK 06D: Here is another variant, but this time the fractions have a common factor. Pupils might initially choose the 4th small mark to the right of 0 for the position of ⅟₁₀, though ⅟₁₀ is clearly not as close to ¼ as that!

 

TASK 06E: This involves the same fractions as in Task 06A, but this time the desired fraction is to the right rather than the left of the given fraction. This might make the task more demanding; pupils will have to imagine, sketch or construct the necessary marks to the right of the ⅟₇ mark.

TASK 06F: Here is a similar task, with the desired fraction to the right of the given fraction, but with the entire 0–1 interval partitioned into equal parts. This should make the task less demanding, as well as perhaps making it easier to explain precisely what is going on.