This theme was inspired by the photo below, which appears on page 108 of an excellent book by Catherine Fosnot and Maarten Dolk (2002): Young Mathematicians at Work: Constructing Fractions, Decimals and Percents.
[My copy is an ex-library book from the University of Winchester. The book is in excellent condition, so did no one ever read it? Perhaps they replaced it with something on Mastery....]
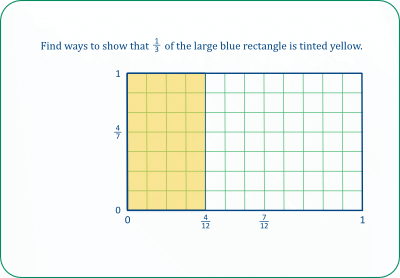
TASK 22A: This is based on the fractions shown in the photo. The book contains several, similar tasks.
A basic way of finding the desired fraction is to count squares: the yellow rectangle covers 12 grid squares, while the blue rectangle covers 72 grid squares. So the fraction is 12/72 = ⅙.
Or: each grid square represents ⅟₇₂ (Why?). So the yellow rectangle represents 12 × ⅟₇₂ = ¹²⁄₇₂ = ⅙.
In the Fosnot and Dolk book, the focus is on multiplying fractions. We can think of the yellow region as ⅜ of ⁴⁄₉ of the blue square (or ⁴⁄₉ of ⅜), so the fraction is ⅜ × ⁴⁄₉ = ¹²⁄₇₂ or ⅙. Fosnot and Dolk make the point that we can also find the fraction by rotating the yellow rectangle (shown here by the pink rectangle), which gives us a new pair of fractions and a new product ⁴⁄₈ × ³⁄₉. Notice that the numerators and denominators are the same as before, but we happen to get 'nicer' fractions leading to this simpler product: ½ × ⅓ = ⅙. Notice too, that the existence of these simpler fractions means it is also easier to see that the pink rectangle covers one 6th of the blue rectangle, as in the diagram below.
Rotating a rectangle as we have done here won't always lead to fractions that can be simplified. However, where it does, as in the current task, it helps to explain how we could get directly from our first product, ⅜ × ⁴⁄₉, to the simpler ½ × ⅓. In effect, this shows that we can extend our rule for simplifying a single fraction (divide the numerator and denominator by a common factor) to simplifying a product of fractions (divide a numerator and the denominator of the same or another fraction by a common factor).
Of course, there are other ways of deriving this rule, for example by using the associative and commutative laws, as here:
⅜ × ⁴⁄₉ = 3×⅛×⅓×⁴⁄₃ = 3×⅓×⅛×⁴⁄₃ = ⅛×⁴⁄₃, and so on.
TASK 22B: Here is a similar task (though not directly from the book).
TASK 22C: Another variant.
15/60 unit squares, or ³⁄₁₀ × ⅚ or ⁵⁄₁₀ × ³⁄₆.
By rotating the rectangle we can see the quarter easily.
TASK 22D: A chance to meet an improper fraction....
TASK 22E: From here on, we go on a bit of a tangent - there are no fractions as such but the maths (which one could think of as involving proportion and scaling) is intriguing.
The previous tasks could be said to use different horizontal and vertical scales - the length of a horizontal unit is different from the length of a vertical unit. The same thing is happening here: while the grid appears to be composed of small squares, they are actually 5 units wide and 7 units high.
The tinted rectangles both cover 10 grid 'squares' so their areas are clearly the same. Each grid square has an area of 5×7 unit squares, so each rectangle has an area of 10×5×7 = 350 unit squares.
Because the axes have different scales, the rectangles are not congruent despite looking as though they are. Their dimensions are 10 by 35 units (yellow) and 25 by 14 units (pink). Of course, 10×35 does not just happen to be the same as 25×14. They are equal because 10×35 = 2×5 × 5×7 has the same factors as 25×14 = 5×5 × 2×7. This is similar to the property of the earlier tasks, where the different pairs of fractions had the same two numerators and the same two denominators.
TASK 22F: These are the same two rectangles as in the previous task, but this time the axes have the same scale. We can see that the rectangles are clearly different. However, as we noted before, their areas are the same because 10×35 and 25×14 are composed of the same factors.
The diagram below-left is the same as the diagram above. The diagram below-right is the 'decompressed' version.
Comments welcome
mietmau@gmail.com
@ProfSmudge