Here we look at the mediant of two fractions a/b and c/d. It is defined as (a+c)/(b+d). It turns out that mediant always lies between the two given fractions but is not necessarily equal to the mean.
When pupils attempt to add two fractions, they sometimes inadvertently find the mediant rather than the sum: the classic ½ + ⅓ = ⅖ misconception. You might feel that introducing pupils to the mediant could reinforce that misconception. On the other hand, the tasks in this theme encourage pupils to think carefully about the size of the fractions involved and thereby should help pupils develop their intuition about how the numerator and denominator affect the size of a fraction. In turn this should help pupils interrogate statements like ½ + ⅓ = ⅖: careful inspection reveals that ⅖ cannot be the sum of ½ + ⅓ since ⅖ is less than one of the addends.
TASK 23A: Here we show the meaning of 'mediant' by means of an example. It should be said that an example alone does not define mediant unequivocally - we could invent other rules that lead to 5/9, given the fractions ⅖ and ¾.
Some pupils will find this task quite challenging. It might not be immediately obvious that the mediant ⁵⁄₉ lies between the given fractions ⅖ and ¾. One way to determine this, of course, is to transform the fractions into equivalent fractions with the same denominator. This can be a useful exercise for some pupils, but is fairly heavy going - the lowest common denominator is 180. Where the primary aim is to order the fractions, it can be illuminating to use 'benchmark' fractions like ⅓, ½, ⅔ and ¾. Pupils might discern that the fraction ⅖ is slightly less than ½ (for example on the basis that 2.5/5 is one half), while ⁵⁄₉ is slightly more than ½; at the same time, ⁵⁄₉ is less than ⁶⁄₉ or ⅔ and so is less than ¾.
TASK 23B: Here we change one of the fractions from Task 23A into an equivalent fraction where the numerator and denominator are much larger - what effect does this have on the mediant?
It turns out that M₁ is the fraction 5/9, and M₂ is 14/21 or 2/3. The position of all four fractions is shown on the blue number line, below. It is not expected that pupils should be as precise- the primary aim is to put the fractions in the correct order. For example, 2/5 will be somewhere to the left of 1/2 (or 2.5/5) and to the right of 1/3 (or 2/6). The fraction 5/9 will be to the right of 2/5 - it is slightly larger than 1/2, but less than 2/3 (or 6/9).
TASK 23C: The fractions are slightly different from the previous task, but still small and fairly familiar, and we consider the mean as well as the mediant - they are usually not the same....
In part a), M₁ is again (slightly) less than M₂. The fraction M₁ is 5/11 (which is slightly less than 1/2) and M₂ is 8/15 (which is slightly more than 1/2).
The mean of fractions A and B is 29/56. How does that compare to 5/11 and 8/15? We could of course use common denominators here, or convert to decimals, but it is also nice to try to make use of benchmark fractions.
As mentioned above, 5/11 is slightly less than 1/2 and 8/15 is slightly more than 1/2 - but so is 29/56. More precisely, 8/15 is 0.5/15 or 1/30 more than 1/2, while 29/56 is only 1/56 more than 1/2. So the mediants and the mean, placed in order, are 5/11, 29/56, 8/15.
TASK 23D: This task emphasises the fact that the mediant and mean are not generally the same. However, they are in one special case - when the denominators are the same.
The lowest common denominator of the two given fractions is 28. If we write the fractions as 8/28 and 21/28, then it is easy to see that the mediant and mean are both 29/56.
TASK 23E: This task is a simple variant on Task 23B: the given fractions are less familiar and more 'extreme'.
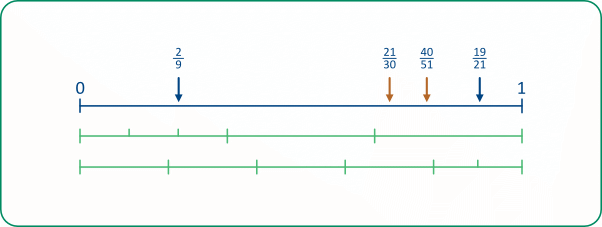
The diagram below shows the position of the four fractions very precisely. However, one wouldn't expect such a precise response from pupils.
One can again get a good estimate by using benchmark fractions. Indeed, this is a rich activity.
For example, one could estimate the position of 2/9 by estimating one third of the line, and then two thirds of that;
the fraction 21/30 is the same as 7/10; it is also slightly larger than 2/3 (21/30 = 2/3 + 1/30);
40/51 is slightly less than 40/50 or 4/5;
19/21 is just 2/21 less than 1, or nearly 1/10.
An alternative is to use decimals:
the four fractions are approximately equal to 0.222, 0.7, 0.784 and 0.905.
It is nice to relate these decimals back to the fractions. For example, one can think of 0.222... as one fifth, plus one fifth of one fifth, plus.... The decimal 0.784 is close to 0.8 which is 4/5. And 0.905 is close to 0.9 which is 1/10 less than 1.
TASK 23F: This task might seem obvious to some pupils, but it won't be to others. It turns out that the mediant is a fraction equivalent to 2/5:
42/105 = (42÷21)/(105÷21) = 2/5.
Formally, we can write this:
a/b and ka/kb are equivalent fractions;
(a+ka)/(b+kb) = a(1+k)/b(1+k) = a/b.
TASK 23G: This is a version of a classic task. It is essentially asking, "What happens to the size of a fraction if we add one to the numerator and the denominator?" At first glance, many pupils will say the size is unchanged.
Another way to approach the task is to think of what happens if we repeatedly add 1 to numerator and denominator. At some stage we would, for example, get the fraction 1040/1100, at another stage the fraction 100040/100100: the fraction gets closer and closer to 1/1. So if we start with a fraction less than 1, it gets larger.
TASK 23H: There is a lot going on here! The tasks refers to fractions as points on the graph. However, fractions are really represented by lines. For example, any point on the line through the origin and point A can be thought of as a fraction equivalent to 2/5, the fraction at A. Note also that the steeper the line, the larger the fraction.
Point M represents the fraction 5/9 which is of course the mediant of the fractions represented by points A and B. The slope of the line through the origin and M lies between the slopes of the lines through the origin and A and the origin and B, so the fraction represented by M lies (somewhere) between the fractions represented by A and B. This will always be the case, for any two given fractions - a nice 'proof' that the mediant of any two fractions always lies between them.
[I remember Ken Ruthven presenting this elegant idea at a conference, which is probably the first time I met it.]
TASK 23I: This is quite advanced! Perhaps more for us as teachers, than for many of our pupils.
It turns out that the mediant of the two given fractions is 5/11 and the mean is 13/30. How can we tell that 5/11 is greater than 13/30? We could use common denominators (giving us 150/330 and 143/330, say). Or we could relate the fractions to one half:
5/11 = 1/2 –0.5/11 = 1/2 – 1/22;
13/30 = 1/2 – 2/30 = 1/2 – 1/15.
So both fractions are less than 1/2 but 5/11 is closer.
This nice task was posted on Twitter by Erick Lee. It inspired my next task, which involves a fraction between ⅛ and ⅟₇.
TASK 23J: This might seem rather strange at first, since we have a part-whole representation of fractions where the whole changes but the part stays the same.
Rectangle A represents ⅛, rectangle C represents ⅟₇ and B represents a fraction in between: ⅟₇.₅ or ²⁄₁₅. The latter is of course the mediant of ⅛ and ⅟₇.
TASK 23K: It is tempting to think that the mediant of ⅛ and ⅟₇ lies exactly halfway between the two fractions, especially as 7.5 is exactly halfway between 8 and 7. We address this in the current task.
The second diagram in this task is interesting. It works well in conveying what was done to rectangles A and C, but because of its small scale it doesn't really allow us to read-off the answer - we have to think it through! The key here is to consider the factors by which A and C are shrunk or stretched. They both change by the same (additive) amount, so proportionally, the smaller rectangle (C), and its tinted region, changes more. So the fraction represented by B (⅟₇.₅) is closer to A's fraction (⅛) than C's fraction (⅟₇).
Numerically, rectangle A is 7.5/8 or about 93.75% of its original width, while C is 8/7.5 or about 106.67% of its original width. 100–93.75=6.25 < 106.67–100=6.67.
To finish things off, it is quite nice to consider our three fractions as decimals (to 4 dp): 0.125, 0.1333, 0.1429.
The difference (to 3 dp) between neighbouring fractions is 0.008 and 0.010, so about one hundredth in each case.
Comments welcome
mietmau@gmail.com@ProfSmudge