D21: Fractions as division (sharing)

 In Theme 13 I looked briefly at how a fraction, in this case ¾, can be thought of as (or as the result of) the division 3÷4. I used the scenario of 3 pancakes shared between 4 people, with this diagram showing some of the ways it could be done:

 

In each of these examples, the objects (pancakes), or parts thereof, are distributed until there is nothing left. In this theme, I consider a slightly different approach, whereby some individuals are given a whole object (be it a pancake, as above, or a bar, as below). Parts of each object are then taken away and given to the individuals who had nothing. Here is the first example:

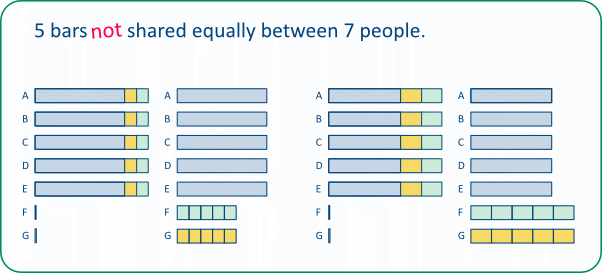
TASK 21A: Here we have the scenario of 5 bars (of some sort!) being shared equally between 7 people. Initially, the 5 bars are given to 5 of the 7 people, with two people having nothing; small, equal parts are now removed from each bar and distributed among the two people with nothing. The critical challenge is to determine how large these pieces should be so that everyone ends up with the same amount.

In the diagram (above) the size of the green and the yellow pieces is such that everyone ends up with the same amount - as can be seen in the third column of the diagram. Everyone gets the equivalent of 5 of the small pieces, and we can see, from the second and third columns, that 7 small pieces make up one bar.
So each piece is ⅟₇ of a bar and everyone gets ⁵⁄₇ of a bar.

I would argue that the diagram can be used to demonstrate this outcome very nicely. Of course, this begs the question of how the certain size of the small pieces was determined in the first place. The diagram below shows what happens if the chosen size of the pieces is slightly too small (left) o slightly too large (right).

TASK 21B: Here we consider a slightly simpler case - only one person is without a bar initially. Again, the diagram should allow pupils to deconstruct what has happened very nicely - this time each small piece is ⅙ of a bar and everyone gets ⅚. We can write the statement below.

5 bars shared between 6 people   =   5 ÷ 6   =   ⅚.

[The statement might seem almost too obvious to bother writing down. However, for younger pupils each of the two steps represents a significant achievement.]

The strength of the task, in particular its diagram, could be said to lie in the ease with which it allows one to analyse the result of a successful sharing process. If you want to encourage students to predict what will happen, as well as analyse the result, you could present them with one of these incomplete or less detailed versions of the diagram:

 or

TASK 21C: Here most pupils will know from the start that each person gets one half of a bar. So the interest in the task is not in finding the answer but in seeing how it emerges as this particular method of sharing plays out. 

The three pieces make ½ because each is ⅙.

TASK 21D: Here we are almost back to the first task, which showed 5 ÷ 7. The current task is perhaps slightly more complex as there are more people who start with nothing.

TASK 21E: This involves the same situation as in the previous task but shows a simpler, more orthodox way of sharing the bars. This time, the bars are cut into pieces before any are distributed and the bars are shared equally one by one among the given number of people. The method involves the same principle as Method 4 at the top of the page. The outcome is not very 'interesting' but the method always works, and shows very clearly how we can get from B ÷ P to B/P:  

P people get 1/P of each bar, and so if there are B bars they get B × 1/P = B/P of a bar altogether.